| CSU |
Hayward |
|
|
Statistics |
Department |
Session 2: Two-State Markov Chains
1. Introduction
Note: This session covers material similar to that in the very
brief Appendix A for Suess, Fraser, and Trumbo:
"Elementary uses of the Gibbs Sampler:
Applications to Medical Screening Tests,"
in STATS #27, Winter 2000.
The main differences are that this session
includes more examples, more detailed explanations,
a few additional topics, and extensive exercises
suitable for instructional use.
Stochastic processes are used to model an extremely wide
variety of real-life situations. A discrete-time stochastic
process is an infinite sequence of random variables,
X(1), X(2), X(3), ...,
usually with some features and structures in common and
viewed as being arranged in time order.
1.1. Two-state processes
In this session an important feature shared by the random variables
X(m) of a process is that each of them can take only two
values 0 and 1. At each step m in time we say that
the process is in one of two states: state 0 or state 1.
Thus each individual (or marginal) random variable has the
probability structure of tossing a (possibly biased) coin — a
Bernoulli distribution.
We will consider two kinds of joint probability structure.
In this section we assume complete mutual independence. In Section 2
we explore the limited kind of dependence typical of a Markov Chain.
1.2. Independence — A strong assumption
If we toss a fair coin repeatedly, then we can say that
P{Tail on mth toss} =
P{X(m) = 0} = 1/2
and
P{Head on mth toss} =
P{X(m)= 1} = 1/2.
If the tosses are collectively independent, then the
probability that the sequence begins HHT is
P{X(1)=1, X(2)=1, X(3)=0} = P{X(1)=1}P{X(2)=1}P{X(3)=0} = (1/2)3 = 1/8.
Furthermore,
P{X(3)=0|X(1)=1, X(2)=1} = P{X(3)=0|X(2)=0} = P{X(3)=0} = 1/2.
More generally,
P{X(3)=k|X(1)=i, X(2)=j} = P{X(3)=k|X(2)=j} = P{X(3)=k} = 1/2,
for i, j, k = 0, 1.
The result on the third toss does not depend in any way on the results
of the tosses that came before. Once the marginal probabilities
P{X(m) = 1} of an independent sequence are known, knowledge
of the past is no guide at all in predicting the future.
Problems:
1.1. In the coin-tossing experiment of this section, find
P{X(1) = 0, X(2) = 0},
P{X(1) = 0, X(3) = 0},
P{X(2) = 0, X(3) = 0} and
P{X(m) = 0, m = 1, ..., 4}.
1.2. Suppose that a fair die is rolled at each step m
and that X(m) = 0 if the roll results
in a 6 and X(m) = 1 otherwise.
(a) Rewrite all four of the equations in this section to fit this situation.
(b) Do problem 1.1 for this situation.
1.3. At step 1 a fair coin is tossed and X(1) takes the
value 0 or 1 as stated in this section. Similarly for step 2 and
X(2). From there on, no additional coin tossing is done:
X(m) takes the same value as X(1) for all
odd values of m and the same value as X(2) for all
even values of m.
(a) Is each random variable independent of the one following
it in the time sequence? Are the random variables collectively
ndependent?
(b) Rewrite the four displayed equations of this section
to fit this situation. (You may need to write more than f
our equations.)
(c) Do problem 1.1 for this situation.
1.4. At step 1 a fair coin is tossed and X(1) takes the
value 0 or 1 as stated in this section. From there on, a fair die
is rolled at each step m = 2, 3, 4, ... . If it shows 6,
then the value of X(m+1) is different than the value of
X(m), otherwise it is the same. For example, starting at
step m = 1, the sequence H6526341 leads to the
X-values 10001111.
(a) Rewrite the last two displayed equations of this section for
this situation. (You may need to write more than two equations.)
[Hint: Use the definition of conditional probability to show that
P{X(3)=0|X(1)=1, X(2)=1} = P{X(1)=1, X(2)=1, X(3)=0}/P{X(1)=1, X(2)=1},
P{X(1)=1, X(2)=1} = P{X(1)=1}P{X(2)=1|X(1)=1},
and so on.]
(b) Do problem 1.1 for this situation. Use the fact that
P{X(1)=0, X(3)=0} = P{X(1)=0, X(2)=0, X(3)=0} + P{X(1)=0, X(2)=1, X(3)=0}.
(c) Are there any two of the random variables in this sequence that
are independent? Explain.
1.5. Suppose you do 100 independent tosses of a coin, not knowing
whether it is fair. If you observe 17 Heads in the 100 tosses, does that
help you to "predict" X(101)? Reconcile your answer with the last
sentence of this section.
1.6. Kim tosses a fair coin, the result is X = 0 for
Tails or X = 1 for Heads. Similarly, Pat tosses a fair
coin independently of Kim, the result is Y = 0 for
Tails or Y = 1 for Heads. The random
variable W is 0 if X and Y both have the
same value, and 1 otherwise. Show that any two of the random
variables W, X, and Y are independent,
but that all three of these random variables are not collectively
independent.
2. Markov Chains
In some practical situations, independence among all steps of a
stochastic process is not a reasonable assumption. For example,
experience with rainfall data from the West Coast of the US has
shown that knowing whether it rains on one day is helpful in
predicting whether it will rain the next. How might we model
the change from clear weather (state 0) one day to rainy weather
(state 1) the next?
2.1. Moving from independence to one-step dependence
The simplest departure from independence is to allow dependence,
but to constrain its extent to dependence on the most recent
available information. We express this idea and define parameters
a and b (with
0 £ a, b £ 1)
by the equations
P{X(m+1)=1|X(m–1)=0, X(m)=0}
= P{X(m+1)=1|X(m–1)=1, X(m)=0}
= P{X(m+1)=1|X(m)=0} = a,
and
P{X(m+1)=0|X(m–1)=0, X(m)=1}
= P{X(m+1)=0|X(m–1)=1, X(m)=1}
= P{X(m+1)=0|X(m)=1} = b,
for any m = 1, 2, 3, ... . That is, the conditional probability of the outcome at step m + 1 does not depend on the outcome at step m – 1 if we know the outcome at step m.
The two probabilities given above are called transition probabilities. They give the conditional probability of making a transition from state i to state j in one step, for i, j = 0, 1, at any point m in time. From a formal point of view, two ideas are involved here, the Markov property and time homogeneity.
2.2. The Markov Property
A formal statement of the Markov Property is as follows: Let
m1, m2,
m3, ..., mL,
mL+1 be distinct steps in time arranged
from earliest to latest. Then
P{X(mL+1)=k|X(mh)=ih, h = 1, ... L–1; X(mL)=j} = P{X(mL+1)=k|X(mL)=j},
for ih, j, k = 0, 1.
Here mL is the last step for which we know the outcome,
which was state j: that is, X(mL) = j.
States at previous steps do not matter. Any information dating from before the
last step for which the state of the process is known is irrelevant in predicting
its state at a later step.
Note: The steps ml are in time order, but they need not be
consecutive. (For example, we might be concerned only with certain odd-numbered
steps m1 = 1, m2 = 5, ...,
mL–1 = 13, mL = 19,
mL+1 = 25.) However, in most of the applications
we have in mind, we look at consecutive steps 1, 2, 3, ... .
This restriction on the relevance of historical information may or may
not be realistic. Here are some examples:
-
If all rain storms are between three and five days in duration, then
it would be foolish to ignore data from the days before yesterday
when predicting whether it will rain tomorrow. However, for West
Coast weather it happens that the Markov property matches reality
reasonably well.
-
If a process describes whether a worker has a white-collar job (0)
or blue-collar job (1) at the end of each month (step), then the
Markov property would clearly be a better assumption than complete
independence, but would ignore some long-term human memory and experience.
For example, consider an accountant who gets fed up with his boss. If he
has skills as an electrician, even from years before, that might influence
his next job transition.
2.3. Time homogeneity
The transition probabilities given in Section 2.1 do not depend on the
step m. We say that the process they describe is time
homogeneous. Intuitively, this means that the transitional
behavior stays the same throughout time.
This assumption may or may not be realistic in a practical
application. In modeling West Coast rain, for example, the
transition probabilities might remain the same throughout
the winter rainy season, but begin to change as we move into spring.
When we speak of a two-state Markov Chain in these
sessions, we will mean a discrete-time stochastic process that
satisfies the Markov Property and is time-homogeneous. For a
two-state chain the two parameters a
and b completely determine the
transitional structure. In Section 3 we will see that
these two parameters also determine the behavior of the chain
far into the future (limiting behavior).
2.4. Trivial and absorbing two-state Markov Chains
In order to avoid some particular situations, we will usually insist
that a and b
must be strictly between 0 and 1: 0 < a, b < 1.
In this section we mention briefly some deterministic and severely
constrained transitional behaviors that occur when this condition
does not hold.
- a = b = 1: We call this the
"flip-flop" process. It simply alternates between states 0 and 1 at successive steps.
There is no chance aspect to this process.
- a = b = 0: We call this
the "never move" process. Whatever its starting state, it stays in that state
throughout all steps. Again here, randomness never enters the picture.
- a = 0, 0 < b < 1:
This is an absorbing process. If the process starts in state 1,
there is a positive probability b at any one step
that it will make a transition to state 0. Once in state 0, it can
never move out; we say that it has been "absorbed" in state 0. The number
of steps until absorption has a geometric distribution with
mean 1/b. (Of course, if the process
starts in state 0, then it is absorbed there from the beginning.)
- b = 0, 0 < a < 1:
This is also an absorbing process; 1 is the absorbing state.
The case in which a = 1, 0 < b < 1
is explored in Problem 2.4.
Problems:
2.1. Recall the process of Problem 1.4: At step 1 a fair coin is tossed
and X(1) takes the value 0 or 1 depending on whether the result in
Tails or Heads, respectively. From there on, a fair die is rolled at each
step m. If it shows 6, then the value of X(m+1) is
different than the value of X(m), otherwise it is the same.
This process satisfies the equations of Section 2.1. What are the
numerical values of a
and b?
2.2. Suppose that for a (homogeneous) Markov Chain
P{X(2) = 1|X(1) = 0} = 0.
(a) Evaluate P{X(3) = 1|X(2) = 0}.
(b) Evaluate P{X(3) = 0|X(1) = 0}.
2.3. Suppose that a Markov Chain for clear weather (0) and rain (1)
has a = 0.1 and
b = 0.5. If it rained yesterday,
what is the probability of rain today? What is the probability of rain
tomorrow? [Hint: Either it rains today or it doesn't.]
2.4. Suppose that a Markov Chain has a = 1
and b = 1/6.
(a) Is it possible to be in state 0 for two successive steps? Is it
possible to be in state 1 for two successive steps?
(b) What is the average number of steps between "visits" to
state 0?
2.5. Suppose that a Markov Chain has
a = b = 1/2.
(a) Does this process differ at all from a process in which a fair
coin is tossed repeatedly and independently with Tails represented
by state 0 and Heads by state 1? Explain.
(b) If a = b = 1/3
does the process differ from independent tosses of a biased coin? What
if a = 1/3 and
b = 2/3?
2.6. Four points around a circle are labeled 0, 1, 2, 3
in clockwise order with 3 adjacent to 0 as well as 2. As the process
begins there is a marker at 0. At each step of a process a fair coin
is tossed. If the result is Heads the marker is moved clockwise one position
(for example, from 0 to 1) and if the result is Tails the marker is
moved counter-clockwise one position (for example, from 0 to 3).
Coin tosses are independent. We say that the X-process is in
state 0 if the marker is at 0, otherwise the process is in
state 1. Show that the Markov Property is violated for this process
by showing that
P{X(m+3)=0|X(m)=0, X(m+1)=1, X(m+2)=1}
differs from
P{X(m+3)=0|X(m)=1, X(m+1)=0, X(m+2)=1}.
Thus the X-process is not a Markov Chain.
3. Transition Matrices
In this section we show how matrix notation can be used to represent the
one-step and multiple-step transition behavior of a Markov Chain. This
notation is useful in deriving the long-term or limiting behavior of a
Markov Chain.
3.1. One-step transition matrix
We adopt the notation pij to denote the conditional
probability of a one-step transition to state i from
state j. That is,
pij = P{X(m+1) = j|X(m) = i},
for i, j = 0, 1, and for any m = 1, 2, 3, ... . For example,
p01 = P{X(m+1) = 1|X(m) = 0} = a.
It is natural to arrange these probabilities pij in a matrix
|
P =
|
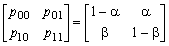
|
. |
Notice that the rows of this matrix sum to 1.
3.2. Multi-step transition probabilities and matrices
The two-step transition probabilities are found by taking into account
whether the chain is in state 0 or state 1 at the intermediate step.
For example,
p01(2) = P{X(3)=1|X(1)=0} = p00p01 + p01p10 = a(2 – a – b).
More generally,
pik(2)= pi0p0k + pi1p1k = Sj pijpjk,
where the sum is taken over j = 0, 1. This means that the two-step transition
matrix P2, consisting of elements pik(2)
can be found as the square of the one-step transition matrix P, using
ordinary matrix multiplication. Specifically, it is not difficult to show that
|
P2 =
|
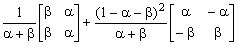 |
, |
where, as usual, the coefficients of a matrix multiply each of its elements
and the sum of two matrices is found by adding corresponding elements. This
may seem to be an unnecessarily complicated way to represent the
matrix P2, but it will prove useful in
Section 4. (See Problem 3.2 for the derivation of this
matrix equation.)
Similarly, the n-step transition matrix Pn is
found by taking the nth power of P. It can be
shown by mathematical induction (see Section 4.3) that
|
Pn =
|
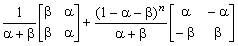 |
. |
Problems:
3.1. Recall the Markov Chain for clear weather (0) and rain (1)
with a = 0.1 and
b = 0.5.
(a) Give the transition matrix P for this chain. Use
numerical entries.
(b) Use matrix multiplication to find P2.
Which element of P2 corresponds to
the probability of rain tomorrow given that it rained yesterday?
Compare with the answer you found in Problem 2.3.
(c) Plug the numerical values of a
and b into the formula
for P2 given in this section, and simplify.
Verify that the result agrees with your matrix in part (b).
3.2. In terms of symbols a and b, verify the formula for P2 given in this section. This requires matrix multiplication and some elementary algebraic manipulation. To start, show that
p00(2) = (1–a)2 + ab = [b + a(1–a–b)2]/(a+b),
and then continue with the other three elements.
3.3. To monitor the flow of traffic, the highway department has a TV camera aimed at the single lane of traffic of a freeway onramp. Each vehicle that passes in sequence can be classified as either a car (0) or a truck (1). Suppose the probability that a car follows a car is 0.8 and the probability that a truck follows a truck is 0.1.
(a) What assumptions are necessary for the car-truck process to be a Markov chain? Write its transition matrix.
(b) If I see a truck in the monitor now, what is the probability that the second vehicle after it will be a truck? The fourth vehicle after it? The eighth? Successively square the transition matrix to get the required higher powers of it.
(c) If I see a car in the monitor now, what is the probability that the second vehicle after it will be a truck? The fourth vehicle after it? The eighth? Use matrices from (b).
(d) Based on what you see in (b) and (c), what do you suppose is the proportion of trucks on this freeway ramp over the long run?
3.4. Mary and John carry out an iterative process involving two urns and two dice. Mary has two urns: Urn 0 contains 2 black balls and 5 red balls; Urn 1 contains 6 black balls and 1 red ball. To begin the process she chooses one of the urns at random, obtaining the value of X(1). She chooses one ball at random from that urn, replaces it, and reports its color to John.
John has two fair dice, one red and one black. The red die has three faces numbered 0 and three faces numbered 1; the black die has one face numbered 0 and five faces numbered 1. John rolls the die that corresponds to the color Mary just reported to him. In turn, he reports the result, X(2) = 0 or 1, to Mary. At step 2 Mary chooses Urn X(2), draws from it and reports the result to John.
The process continues, giving X(3), X(4), and so on. Notice that each step requires two random events, a draw from one of the urns and a roll of one of the dice. Also notice that at any one point only the result of the last draw from an urn is relevant to John, or only the result of the last roll of a die is relevant for Mary.
The X-process is a Markov Chain. Find its transition matrix.
4. Limiting Behavior of a Markov Chain
In this section we see that certain Markov Chains "settle down" to a limit in the long run. The expression for the multi-step transition matrix given in Section 3 is the key to this discussion.
4.1. The limit of the multi-step transition matrix
Recall the expression for the matrix Pn
in Section 3:
|
Pn =
|
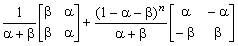 |
, |
and define
D = 1 – a – b.
In addition, we require that the one-step transition matrix P
must have all positive elements. That is,
0 < a, b < 1
or |D| < 1.
This is the condition we discussed in Section 3.4.
The first term in the expression for Pn does
not depend on n. The second term depends on n only
by way of the exponent in the constant (scalar) multiplier. Under the
condition that |D| < 1, the
second term vanishes as n increases. So the first term is the
imit as n approaches infinity:
|
lim Pn =
|
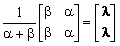 |
, |
where the row vector l =
[l0,
l1] =
[b/(a + b), a/(a + b)].
For example, p01(n)
approaches l1 = a/(a + b).
There are two important things to notice about this limiting process.
-
The rate of convergence is "geometric." This means that, unless
|D| is very nearly equal to 1,
convergence is quite rapid. Thus for moderately large values of n,
we might use the limit as an approximation to Pn. For
example, p01(n) is nearly equal to
a/(a + b)
for moderately large values of n.
-
Both rows of the limiting matrix are the same.
Recall that the top row governs long-term transitions
when the initial state is state 0 and the bottom
row governs transitions from state 1. This means that,
in the long run, the starting state does not matter. For example, both
p01(n) and p11(n)
approach the same value
a/(a + b).
In the long run, a Markov Chain with |D| < 1 settles down to a limiting distribution that does not depend on its starting point. Roughly speaking, one might say that the "one-stage" Markov dependence eventually wears off and the process "forgets" where it started. In symbols,
P{X(¥
) = 0} = b/(a + b) and P{X(¥
) = 1} = a/(a + b).
Notice that these are unconditional probabilities, because the initial state does
not matter in the limit. The vector l is called
the limiting distribution of the chain.
4.2. A alternate computation of the limiting distribution
An alternative way to find the limiting distribution is to solve the matrix equation
lP = l.
This matrix equation is equivalent to two linear equations
l
0 = l0(1–a) + l1b and l1 = l0a + l1(1–b),
which are colinear because they each reduce to l0a = l1b. But because l0 + l1 = 1 we have the solution l0 = b/(a+b) and l1 = a/(a+b), which agrees with the result already obtained from the limiting argument at the end of Section 4.2.
Intuitively, the idea behind the "steady state" matrix equation of the previous paragraph is that the probability distribution attains a stationary condition in the limit. Thus at steady state the probability l0 of being in state 0 ought to be the sum of the probability l0(1–a) of "arriving from" state 0 on the previous step and the probability (1–l0)b of arriving from state 1 on the previous step.
4.3. Proof by induction
The proof of the expression for Pn
stated at the end of Section 3.2 is outlined very briefly here,
with most of the work relegated to Problem 4.4. This is a proof
by mathematical induction and so it has two parts:
-
The initial step. We need to verify that the stated formula for
Pn is valid for the case n = 1.
Upon substituting 1 for n in the formula and simplifying,
one obtains the expression for the one-stage transition matrix P.
-
The induction step. Multiply the expression for Pn
by P and verify that the result simplifies to the corresponding
expression for Pn+1:
|
Pn+1 =
|
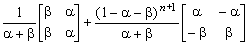 |
. |
Problems:
4.1. Once again, recall the Markov Chain for clear weather (0) and rain (1) with a = 0.1 and b = 0.5.
(a) Find the limit of Pn and use it to find the
limiting distribution l. Also find
the limiting distribution by solving the matrix equation
lP = l.
Over the long run what proportion of the days will be rainy.
(b) Suppose it is raining today. Compare the exact probability of rain 16 days from now with the limiting approximation.
(c) Compare this process with the process consisting of independent trials and having the same proportion of rainy days. In particular, what is the average length of runs of rainy days for each process.
(d) Suppose that rainy days at another place are governed by a Markov Chain with a = 0.15 and b = 0.75. How does this chain differ from the one specified in (a)? In particular, which of the answers (a)-(c) change substantially?
(e) Repeat (d) with a = 0.01 and b = 0.05.
4.2. Find the limiting distribution of a two-state Markov Chain
having a = 0.0123 and
b = 0.6016. This particular chain will be used in a later session in connection with an elementary illustration of the Gibbs Sampler.
(a) What is its limiting distribution.
(b) If you observed this chain for 10,000 steps, about how many visits to state 1 would you expect to observe?
(c) If you observed this chain for 10,000 steps, about how many
(one-step) transitions from state 1 to state 0 would you
expect to observe? About how many transitions from state 0 to
state 1? [Be careful, the first answer is nowhere near 6016.]
4.3. What is the limiting (and stationary) distribution of the chain in Problem 3.3 (cars and trucks)? In Problem 3.4 (urns and dice)?
4.4. Finish the induction proof of the expression for Pn.
(a) Verify the initial step.
(b) Verify the induction step. This is somewhat similar to Problem 3.2.
Further Reading
Only two-state Markov Chains have been covered in this session
because they suffice as background for later sessions in this series.
Markov Chains with larger finite and infinite state spaces are covered
in very many undergraduate and graduate textbooks on introductory
probability theory and stochastic processes. Additional interesting
issues arise for chains with more than two states, such as the grouping
of states into persistent (recurrent) and transient (non-recurrent)
intercommunicating classes and the possibility of nondeterministic
periodicities. Quiz Question 15
on this site has some examples.
Here are some specific references to books with elegant treatments
of Markov Chains:
- One reference that gives a careful proof of the limit theorem for a k-state chain is W. Feller: An introduction to probability theory and its applications, Vol. 1 (3rd ed.), 1950, Wiley, New York.
- Cox and Miller: The theory of stochastic processes, 1965, Wiley, New York gives a treatment of two-state chains that begins at about the level of this session and uses similar notation, but also includes a discussion of the multi-step transition matrix in terms of the theory of linear algebra (using eigenvectors). Cox and Miller's book also includes treatments of more advanced Markov Chains.
- Roe Goodman: Introduction to stochastic models, 1988, Benjamin-Cummings, Menlo Park, CA. Chapter 6 treats Markov Chains with a heavy emphasis on ideas from linear algebra. Some of the notation and counting conventions differ from those of other texts.
- Kai Lai Chung: Markov Chains with stationary transition probabilities, Springer, 1960, Berlin, is a more specialized and advanced treatise. (Chung uses stationary where we have used homogeneous.)
The article on Gibbs Sampling in STATS magazine mentioned in the note
at the beginning of this article and the companion
Appendix A (published on the web, but not printed with the article) are copyright © 2000 by the American Statistical Association.
This document, Session 2, is copyright © 1999, 2000 by Bruce E. Trumbo.
All rights reserved. Please contact the author btrumbo@csuhayward.edu
to obtain permission for instructional and other uses. This is a draft; comments and corrections are welcome.