Appendix A: Convergence of a Two-State Markov Chain

CSU	Hayward
	Statistics	Department

Appendix A: Convergence of a
Two-State Markov Chain

Two-state chains that stabilize to a limit

Let X(1), X(2), X(3), ... be a homogeneous Markov chain with two possible states, 0 and 1. Its one-step transition matrix can be expressed as

For example, p₀₁ = P{X(2)=1|X(1)=0}= a is the probability of making a transition from state 0 to state 1 in one step. Also, for any starting step m = 1, 2 ..., the homogeneity and Markov properties imply, respectively, that

p₀₁ = P{X(m+1)=1|X(m)=0} = a

and that

p₀₁ = P{X(m+2)=1|X(m)=i, X(m+1)=0} = a, for i = 0, 1.

It is not difficult to show that if P has all positive elements (0 < a, b < 1), then the probability structure of the chain stabilizes to a limit as the number of stages increases—and to find what that limit must be. Our purpose here is to sketch a proof of these results.

Multi-stage transition probabilities

The two-step transition probabilities are found by taking into account whether the value of the chain at the intermediate step is 0 or 1. For example,

p₀₁(2) = P{X(3)=1|X(1)=0} = p₀₀p₀₁ + p₀₁p₁₁ = a(2 – a – b).

The probabilities of two-step transitions from 0 to 0, 1 to 0, and 1 to 1 are found similarly. Thus, the two-step transition matrix is P² (obtained by ordinary matrix multiplication). By induction (see the section below), the n-step transition matrix Pⁿ can be expressed as the sum of two matrices:

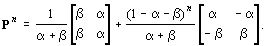
The first term in this sum does not depend on n. The second depends on n only via the exponent in the constant (scalar) multiplier; this term vanishes as n approaches infinity provided that |D| = |1 – a – b| < 1, which is guaranteed by our original restriction that all elements of P be positive. This result not only shows that Pⁿ converges to a limit but also that the convergence takes place at a relatively rapid "geometric" rate.

Technical notes: Here we focus on cases were P has all positive elements. However, the P-matrix for a so-called ergodic two-state chain either has all positive elements or has one of a and b (but not both) equal to 1. This is equivalent to saying that P² has all positive elements. The condition |D| < 1 required for convergence above includes not only ergodic chains, but also the "absorbing" cases (either a or b, not both, equal to 0), which have degenerate limiting distributions.

The upper-right element of the matrix Pⁿ is the n-step transition probability p₀₁(n) = P{X(n+m)=1|X(m)=0}. We have just seen that, as n approaches infinity, p₀₁(n) approaches a/(a + b). Similarly, looking at the lower-right element of Pⁿ, we find that p₁₁(n) also approaches a/(a + b). In the long run, such a Markov chain "forgets" where it started. Regardless of the starting value of the process, in the long run we have simply p = P(X(¥) = 1) = a/(a + b). Similarly, looking at the elements in the first column of Pⁿ, we have the long-run probability p* = P{X(¥) = 0} = b/(a + b). We say that the limiting distribution of X is given by the vector

l = (p*, p) = (b/ (a + b), a/(a + b)).

A matrix equation for the limiting distribution

An alternative way to obtain this limiting distribution, when it exists, is to solve the matrix equation lP = l. This matrix equation yields two linear equations:

p* = p*(1 – a) + pb and p = p*a + p(1 – b).

These equations are co-linear. Together with the requirement that p + p* = 1, either one of them yields p = a/(a + b) and p* = b/(a + b). These are the same results we obtained from the limiting argument above.

For example, let a = 0.0123 and b = 0.6016, so that 1/(a + b ) = 1 / 0.6139 = 1.6289, and the limit is

This shows the limit of a particular matrix, but also illustrates the principle that when Pⁿ approaches a limit, each row of the limit P^¥ is the same as the solution l = (p*, p ) of the matrix equation lP = l.

Proof by induction

The proof of the expression for Pⁿ as the sum of two matrices is by induction, using simple algebra. The initial step is to verify that this expression simplifies to P when n = 1. The induction step is to multiply this expression for Pⁿ by P, and to verify that the result simplifies to

Example: Markov weather

Suppose that on a tropical island each day can be classified as sunny (0) or rainy (1). The weather tomorrow depends only on the weather today. If it is sunny today, the probability of rain tomorrow is a = 0.1; if it is rainy today, it will be sunny tomorrow with probability b = 0.4. Then our results above show that it rains on p = 20% of the days over the long run.

In this particular Markov-dependent pattern, rainy days tend occur in "runs" to a much greater extent than they would if rain on each day were independent of the weather on the previous day. While a knowledge of today's weather helps considerably in predicting tomorrow's weather, it does little more good than the 20% rule in predicting weather 10 days from now: |D|¹⁰ = (1 – a – b)¹⁰ = 0.001, so that the first term of our expression for P¹⁰ predominates enormously over the second term.