library(pacman)
p_load(tidyverse, fpp3)Forecasting Models
Models
global_economy# A tsibble: 15,150 x 9 [1Y]
# Key: Country [263]
Country Code Year GDP Growth CPI Imports Exports Population
<fct> <fct> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 Afghanistan AFG 1960 537777811. NA NA 7.02 4.13 8996351
2 Afghanistan AFG 1961 548888896. NA NA 8.10 4.45 9166764
3 Afghanistan AFG 1962 546666678. NA NA 9.35 4.88 9345868
4 Afghanistan AFG 1963 751111191. NA NA 16.9 9.17 9533954
5 Afghanistan AFG 1964 800000044. NA NA 18.1 8.89 9731361
6 Afghanistan AFG 1965 1006666638. NA NA 21.4 11.3 9938414
7 Afghanistan AFG 1966 1399999967. NA NA 18.6 8.57 10152331
8 Afghanistan AFG 1967 1673333418. NA NA 14.2 6.77 10372630
9 Afghanistan AFG 1968 1373333367. NA NA 15.2 8.90 10604346
10 Afghanistan AFG 1969 1408888922. NA NA 15.0 10.1 10854428
# … with 15,140 more rowsglobal_economy %>% filter(Country == "Italy") %>%
autoplot()Plot variable not specified, automatically selected `.vars = GDP`
gdppc_Italy <- global_economy %>%
filter(Country == "Italy") %>%
mutate(GDP_per_capita = GDP / Population)
gdppc_Italy %>% autoplot(GDP_per_capita)
Train the model (estimate)
gdppc <- global_economy %>%
mutate(GDP_per_capita = GDP / Population)
fit <- gdppc %>%
model(trend_model = TSLM(GDP_per_capita ~ trend()))Warning: 7 errors (1 unique) encountered for trend_model
[7] 0 (non-NA) casesfit # A mable: 263 x 2
# Key: Country [263]
Country trend_model
<fct> <model>
1 Afghanistan <TSLM>
2 Albania <TSLM>
3 Algeria <TSLM>
4 American Samoa <TSLM>
5 Andorra <TSLM>
6 Angola <TSLM>
7 Antigua and Barbuda <TSLM>
8 Arab World <TSLM>
9 Argentina <TSLM>
10 Armenia <TSLM>
# … with 253 more rowsForecasts
fit %>% forecast(h = "3 years")# A fable: 789 x 5 [1Y]
# Key: Country, .model [263]
Country .model Year GDP_per_capita .mean
<fct> <chr> <dbl> <dist> <dbl>
1 Afghanistan trend_model 2018 N(526, 9653) 526.
2 Afghanistan trend_model 2019 N(534, 9689) 534.
3 Afghanistan trend_model 2020 N(542, 9727) 542.
4 Albania trend_model 2018 N(4716, 476419) 4716.
5 Albania trend_model 2019 N(4867, 481086) 4867.
6 Albania trend_model 2020 N(5018, 486012) 5018.
7 Algeria trend_model 2018 N(4410, 643094) 4410.
8 Algeria trend_model 2019 N(4489, 645311) 4489.
9 Algeria trend_model 2020 N(4568, 647602) 4568.
10 American Samoa trend_model 2018 N(12491, 652926) 12491.
# … with 779 more rowsfit %>%
forecast(h = "3 years") %>%
filter(Country == "Italy") %>%
autoplot(gdppc) +
labs(y = "$US", title = "GDP per capita for Sweden")
Simple forecasting methods
aus_production %>% filter_index("1970 Q1" ~ "2004 Q4")# A tsibble: 140 x 7 [1Q]
Quarter Beer Tobacco Bricks Cement Electricity Gas
<qtr> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl>
1 1970 Q1 387 6807 386 1049 12328 12
2 1970 Q2 357 7612 428 1134 14493 18
3 1970 Q3 374 7862 434 1229 15664 23
4 1970 Q4 466 7126 417 1188 13781 20
5 1971 Q1 410 7255 385 1058 13299 19
6 1971 Q2 370 8076 433 1209 15230 23
7 1971 Q3 379 8405 453 1199 16667 28
8 1971 Q4 487 7974 436 1253 14484 24
9 1972 Q1 419 6500 399 1070 13838 24
10 1972 Q2 378 7119 461 1282 15919 34
# … with 130 more rows# Set training data from 1992 to 2006
train <- aus_production %>%
filter_index("1992 Q1" ~ "2006 Q4")
# Fit the models
beer_fit <- train %>%
model(
Mean = MEAN(Beer),
`Naïve` = NAIVE(Beer),
`Seasonal naïve` = SNAIVE(Beer)
)
# Generate forecasts for 14 quarters
beer_fc <- beer_fit %>% forecast(h = 14)
# Plot forecasts against actual values
beer_fc %>%
autoplot(train, level = NULL) +
autolayer(
filter_index(aus_production, "2007 Q1" ~ .),
color = "black"
) +
labs(
y = "Megalitres",
title = "Forecasts for quarterly beer production"
) +
guides(colour = guide_legend(title = "Forecast"))Plot variable not specified, automatically selected `.vars = Beer`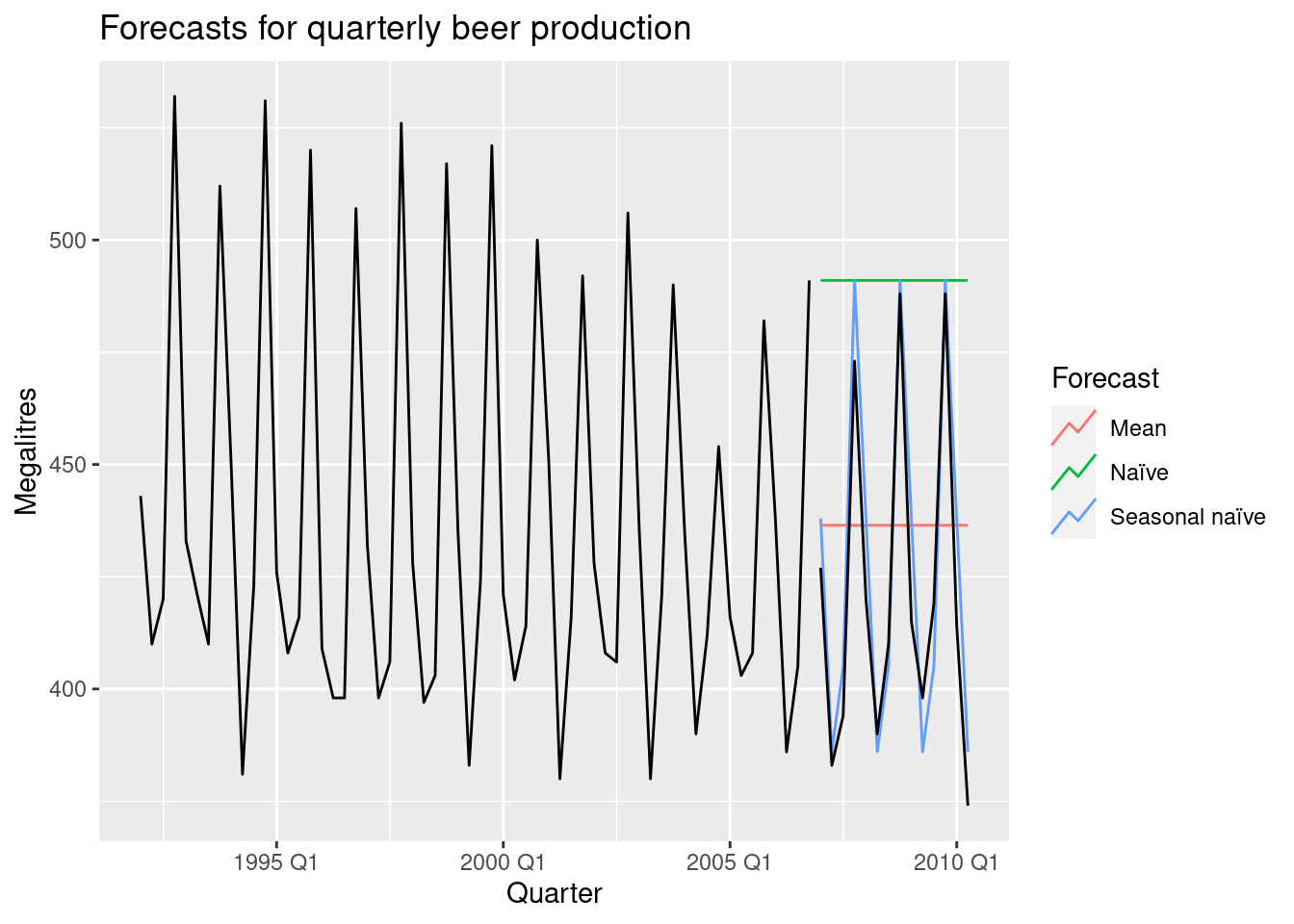
Residuals and Fitted Values
aug <- augment(beer_fit)
aug# A tsibble: 180 x 6 [1Q]
# Key: .model [3]
.model Quarter Beer .fitted .resid .innov
<chr> <qtr> <dbl> <dbl> <dbl> <dbl>
1 Mean 1992 Q1 443 436. 6.55 6.55
2 Mean 1992 Q2 410 436. -26.4 -26.4
3 Mean 1992 Q3 420 436. -16.4 -16.4
4 Mean 1992 Q4 532 436. 95.6 95.6
5 Mean 1993 Q1 433 436. -3.45 -3.45
6 Mean 1993 Q2 421 436. -15.4 -15.4
7 Mean 1993 Q3 410 436. -26.4 -26.4
8 Mean 1993 Q4 512 436. 75.6 75.6
9 Mean 1994 Q1 449 436. 12.6 12.6
10 Mean 1994 Q2 381 436. -55.4 -55.4
# … with 170 more rowsautoplot(aug, .innov) +
labs(x = "Day", y = "Residual",
title = "Residuals")Warning: Removed 5 row(s) containing missing values (geom_path).
aug %>%
ggplot(aes(x = .innov)) +
geom_histogram() +
labs(title = "Histogram of residuals")`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.Warning: Removed 5 rows containing non-finite values (stat_bin).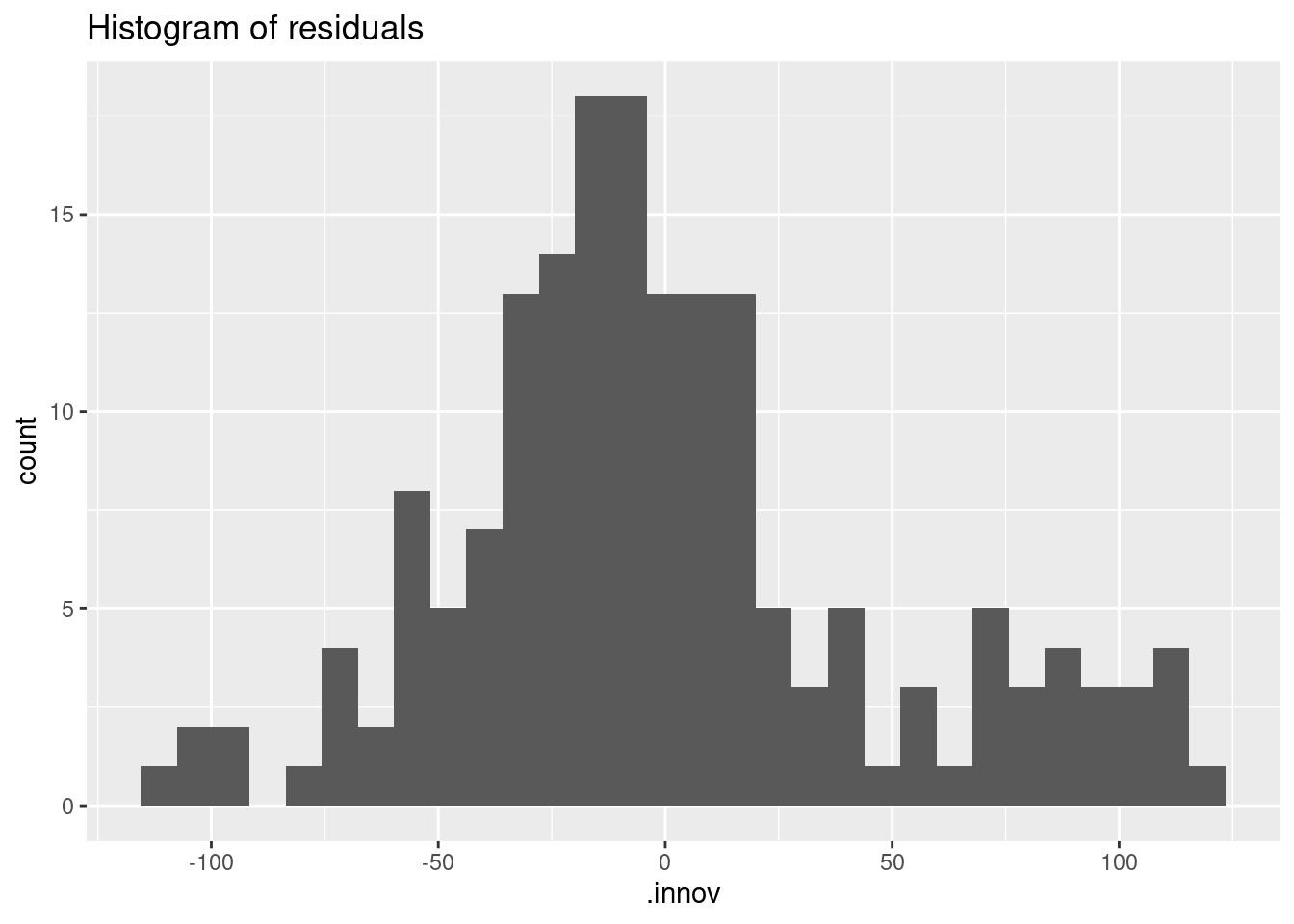
aug %>%
ACF(.innov) %>%
autoplot() +
labs(title = "ACF of residuals")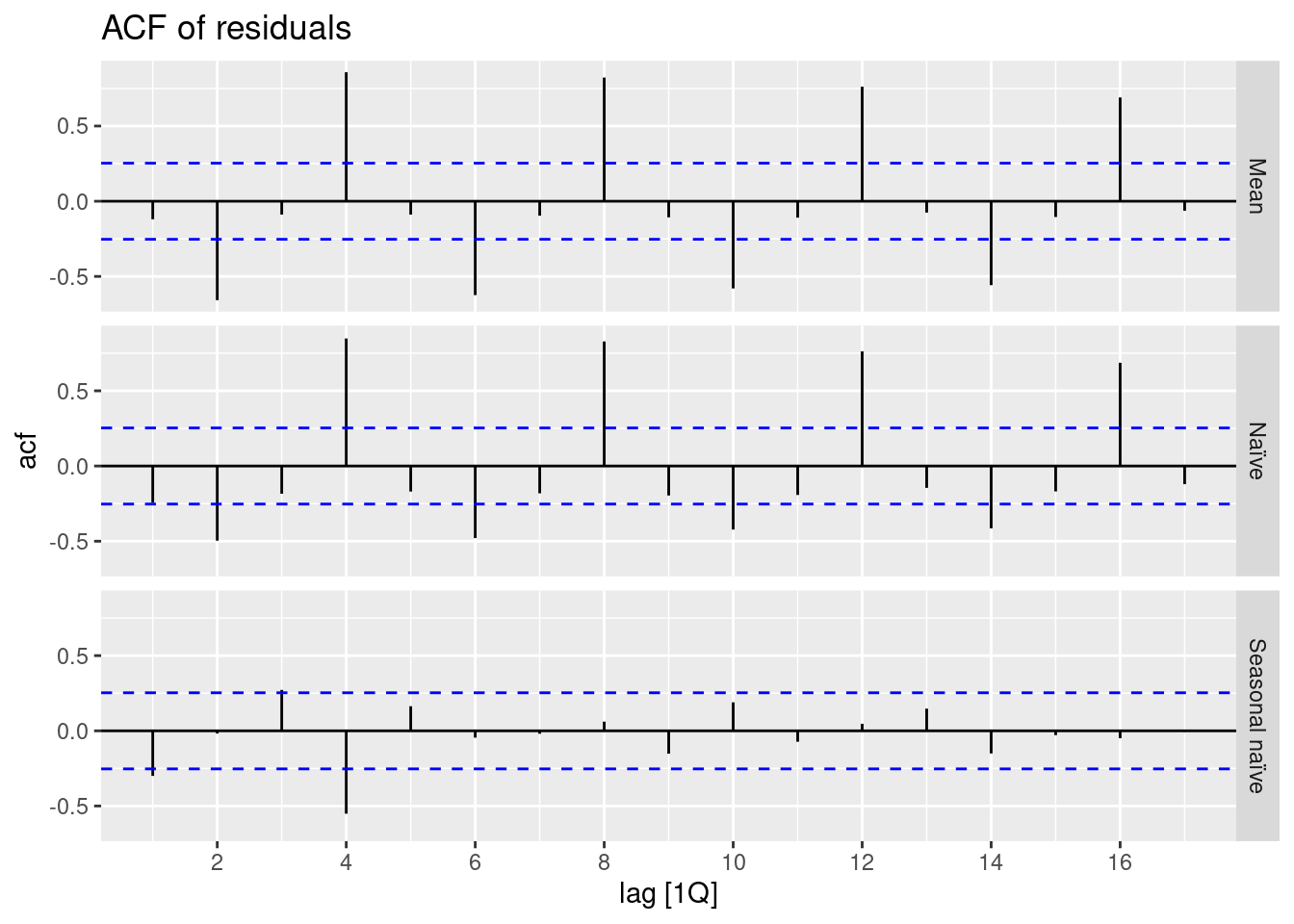
aug %>% features(.innov, box_pierce, lag = 10)# A tibble: 3 × 3
.model bp_stat bp_pvalue
<chr> <dbl> <dbl>
1 Mean 157. 0
2 Naïve 133. 0
3 Seasonal naïve 31.3 0.000515aug %>% features(.innov, ljung_box, lag = 10)# A tibble: 3 × 3
.model lb_stat lb_pvalue
<chr> <dbl> <dbl>
1 Mean 180. 0
2 Naïve 153. 0
3 Seasonal naïve 35.1 0.000122