Appendix B: Brief Intro. to Bayesian Inference

CSU	Hayward
	*Statistics*	*Department*

Session 4: A Brief Introduction
To Bayesian Estimation

Note: This session is intended to be a free-standing introduction to certain aspects of Bayesian inference. The material is of interest in its own right, but is also necessary background for Session 4. This session expands considerably upon the very brief Appendix B for Suess, Fraser, and Trumbo: "Elementary Uses of the Gibbs Sampler: Applications to Medical Screening Tests," in STATS #27, Winter 2000. It contains more examples, more detailed explanations, some additional topics, and extensive exercises suitable for instructional use. For another introduction to Bayesian inference, see the article by Hal Stern: "A Primer on the Bayesian Approach to Statistical Inference," in STATS #23, Fall 1998, pages 3-9.

3.1. Introduction

Bayesian and frequentist statistical inference take fundamentally different viewpoints toward statistical decision making. The frequentist view of probability, and thus of statistical inference, is based on the idea of an experiment that can be repeated very many times. The Bayesian view of probability and of inference is based on personal assessments of probability and on data from a single performance of an experiment. In practical application, both ways of thinking have advantages and disadvantages, some of which we will explore here.

Statistics is a young science. For example, interval estimation and hypothesis testing have become common in scientific research and business decision making only within the past 75 years, and then only gradually. On this time scale it seems strange to talk about "traditional" approaches. Nevertheless, frequentist viewpoints are currently much better established, particularly in scientific research, than Bayesian ones. Recently, the use of Bayesian methods has been increasing, partly because improvements in computation have made these methods easier to apply in practice and partly because the Bayesian approach seems to be able to get useful solutions in some applications where frequentist approaches cannot. The Gibbs sampler, examined more fully in Session 4, is one example of a broadly applicable, computationally intensive Bayesian method.

We will see later on that, for the very simple examples considered here, Bayesian and frequentist methods give similar results. But that is not the main point. We hope you will gain some appreciation that Bayesian methods are sometimes the most natural useful ones in practice.

For most people, the starkest contrast between frequentist and Bayesian approaches is that Bayesian inference provides the opportunity — even makes it a requirement — to take into account "information" that is available before any data is collected. That is where we begin.

3.2. Prior Distributions: Personal Opinions and Expert Knowledge

The Bayesian approach to statistical inference treats population parameters as random variables (not as fixed, unknown constants). The distributions of these parameters are called prior distributions. Often both expert knowledge and mathematical convenience play a role in selecting a particular type of prior distribution.

3.2.1. Example 1: Election polling

Suppose that Proposition A is on the ballot for an upcoming statewide election, and that a political consultant has been hired to help manage the campaign for its passage. The proportion P of prospective voters who currently favor Proposition A is the population parameter of interest here. Based on her knowledge of the politics of the state, the consultant's judgment is that the proposition is almost sure to pass, but not by a large margin. She believes that the most likely proportion of voters in favor is 55% and that the percentage is not likely to be below 51% or above 59%.

It is reasonable to consider the beta distribution to model the expert's opinion of the proportion in favor because distributions in the beta family take values in the interval (0, 1) as do proportions. This family of distributions has density functions of the form

f(p) = K₁p^a^–1(1 – p)^b–1, 0 < p < 1.

where a, b > 0, and where K₁ is a constant chosen so that f(p) integrates to 1 over (0, 1).

A member of the beta family that corresponds roughly to the expert's opinion has a = 331 and b = 271.

o This density curve has its mode at (a – 1) / (a + b – 2) = 0.55.

o Numerical integration shows that P(0.51 < P < 0.59) = 0.95.

Of course, many other distributional shapes share these two numerical properties, but we choose a member of the beta family because it makes the mathematics relatively easy and because we have no reason to believe its shape is inappropriate here.

If the political consultant's judgments about the political situation are correct, then they may be helpful in managing the campaign. If she too often brings bad judgment to her clients, her reputation will suffer and she will be out of the political consulting business before long. Fortunately, as we will see, the details of her judgments become less important if we also have polling data to rely upon.

3.2.2. Example 2: Weighing an object

A construction company buys steel beams with a nominal weight of 200 lb. Experience with a particular supplier of these beams has shown that their beams very seldom weigh less than 180 or more than 220 lb. In these circumstances it may be convenient and reasonable to suppose that the distribution of weights of beams from this supplier is normal with mean 200 and standard deviation 10.

Usually, the exact weight of a beam is not especially important, but there are some situations in which it is crucial to know the weight of a beam more precisely. Then a particular beam is selected and weighed several times on a scale. The scale is known to give results that are normally distributed without bias, but with a standard deviation of 1 lb. Here it seems reasonable to use N(200, 10²) as the prior distribution of the weight m of a beam. The hope is that the weighing process will help us to know its true weight more accurately.

Theoretically, the frequentist statistician would ignore "prior" or background experience in doing statistical inference, basing statistical decisions only on the data collected when a beam is weighed. In real life it is not so simple. For example, the design of the weighing experiment will very likely take past experience into account in one way or another. For the Bayesian statistician the explicit codification of some kinds of background information into a prior distribution is a required first step.

3.2.3. Example 3: Counting mice

An island in the middle of a river is one of the last known habitats of an endangered kind of mouse. The mice rove about the island in ways that are not fully understood and so are taken as random. Ecologists are interested in the average number of mice to be found in particular regions of the island. To do the counting in a region they set many traps there at night, using bait that is irresistible to mice at close range. In the morning they count and release the mice caught. It seems reasonable to suppose that almost all of the mice in the region the previous night were caught and that the number of them on any one night has a Poisson distribution. The purpose of the trapping is to estimate the mean l of this distribution.

Even before the trapping is done the ecologists doing this study have some information about l. For example, even though the mice are quite shy, there have been occasional sightings of them in almost all regions of the island, so it seems likely that l > 1. On the other hand, from what is known of the habits of the mice and the food supply in the regions, it seems unlikely that there would be as many as 25 of them in any one region at a given time. In these circumstances, it may be reasonable to use a gamma distribution with shape parameter a = 4 and scale parameter b = 3 as a prior distribution for values l of the random variable L. This gamma distribution has density function f(x) = K₁ x^a–1e^–^bx (for x > 0), mean ab = 12, mode (a – 1)b = 9, variance ab² = 36, and standard deviation 6.

A member of the gamma family may be a reasonable prior because l must be positive and members of the gamma family take only positive values. We will see later that choosing a gamma prior simplifies some important mathematical computations.

These technicalities of the prior distribution aside, it is clear that the experience of the ecologists with the island and its endangered mice will influence the course of this investigation in many ways: dividing the island into meaningful regions; modeling the randomness of mouse movement as Poisson, the number of traps to use and where to place them, what to use for bait so as to attract mice from a region of interest but not from all over the island, and so on. The expression of some of their background knowledge as a prior distribution is perhaps a relatively small use of their expertise. But it is a necessary first step in Bayesian inference, and it is perhaps the only aspect of their expert opinion that will be explicitly tempered by the data that are collected.

Problems

3.2.1. In Example 1, show that for appropriate values of a and b, the density function has a unique mode at (a – 1)/(a + b – 2). [Hint: Differentiate the density function, set the derivative equal to 0, and note the values of a and b for which the solution of this equation yields an absolute maximum.]

3.2.2. In Example 3, verify the stated value of the mode, and say for what values of a and b the mode exists.

3.2.3. In Example 1, suppose that a = 2 and b = 1. Find the value of the constant K₁ that makes this beta density function integrate to 1. Find the mean and variance. Find the values a and b such that P(P < a) = P(P > b) = 0.025. Sketch the density function. Repeat for a = 1 and b = 1

3.2.4. In Example 3, suppose that a = 1 and b = 10. Find K₁, E(L), V(L), and a and b such that P(L < a) = P(L > b) = 0.025.

3.2.5. For each of the three examples of this section sketch the given prior distribution (for the specific parameter values stated). Then use tables, Minitab, S-Plus, or other statistical software to find values a and b that cut off the upper and lower 2.5% of the stated prior distributions. Shade in the corresponding areas. An example of a typical Minitab instruction is as follows:

MTB > invcdf 0.975;
SUBC> beta 331 271.

For Example 2, it is obvious that the true weight cannot be negative. Why is it safe to ignore the fact that the suggested normal prior distribution includes negative values?

3.2.6. Suggest reasonable prior distributions in the following cases:

(a) In Example 1, suppose that a very successful professional political fundraiser from another state has been hired. He doesn't know what Proposition A is about and has no experience with the politics of this state. Before he sees some polling data he has absolutely no idea what percentage of the voters favor Proposition A.

(b) In Example 2, the mean weight of the beams from the supplier is around 200 lb. and we suppose that about half of them weigh between 195 and 205 lb.

(d) In Example 1, now suppose the fundraiser is unfamiliar with opinions in the state, does know what Proposition A is about, is sure that it will be extremely controversial with a very low probability that the percentage in favor is anywhere near 1/2, but he has no opinion whether the sentiment will be overwhelmingly for or overwhelmingly against. (Suggest general ranges of parameter values.)

3.3. Data and Posterior Distributions

The second step in Bayesian inference is to collect data and to combine the information in the data with the expert opinion represented by the prior distribution. The result is a posterior distribution that can be used for inference. The computation of the posterior distribution uses Bayes' Theorem. You have probably seen Bayes' Theorem stated for an event E and a partition {B₁, B₂, ..., B_k} of a sample space S. (The B_i are mutually exclusive events whose union is S):

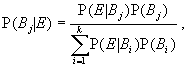
for j = 1, ..., k. Even in this most elementary setting, the quantities P(B_j) are called prior probabilities and P(B_j|E) are called posterior probabilities.

A more general version of Bayes' Theorem for distributions involving data x and a parameter p is as follows:

where the integral is taken over the region where the integrand is positive. The denominator of this fraction is a constant J. The conditional density f(p|x) is the posterior distribution of P given X, evaluated for the specific numerical values X = x and P = p.

3.3.1. Example 1 (election) continued.

In our election example, suppose n = 1000 subjects are selected at random. Assuming the specific parameter value P = p, the number X of them in favor of Proposition A is a random variable with the binomial distribution

f(x|p) = K₂ p^x(1 – p)ⁿ^–x,

for x = 0, 1, 2, ..., n, and where K₂ = n!/[x!(n–x)!] is the constant that makes the distribution sum to 1. Then the general version of Bayes' Theorem gives the posterior distribution

f(p|x) = K₃p^x(1 – p)ⁿ^–x p^a^–1(1 – p)^b–1 = K₃p^x⁺^a–1(1 – p)ⁿ^–x+^b–1,

where K₃ = K₁K₂/J. If x = 621 of the n = 1000 subjects interviewed favor Proposition A, it is then clear that the posterior has a beta distribution with parameters x + a = 952 and n – x + b = 650. According to this posterior distribution, P(0.570 < P < 0.618) = 0.95, so that a 95% posterior probability interval for the percent in favor is (57.0%, 61.8%).

Note the following three aspects of this development:

o The interval estimate for P is a straightforward probability statement. Unlike frequentist "confidence intervals," it does not require the user to imagine a repeatable experiment.

o The mathematical forms of the beta prior and the binomial data are similar, making it especially easy to find the posterior. In such cases we say that the beta is a "conjugate prior" to the binomial.

Often in Bayesian distributional computations it is unnecessary to know the actual values of the constants involved. Then the proportionality symbol µ can be used to show relationships. For example, the first equation in this subsection could have been written as f(x|p) µ p^x(1 – p)ⁿ^–x, where the expression on the right is the kernel of the density function. The kernel is the part of a density function that displays necessary variables and parameters, but does not display the constant of integration.

3.3.2. Example 2 (weighing a beam) continued.

Suppose that a particular beam is selected from among the beams available. The prior distribution is N(200, 10²) and so f(m) µ exp [(m – m₀)²/t²], where m₀ = 100 and t = 10. The data x = (x₁, ..., x₅) provide the likelihood function

f(x|m) µ exp {–S[(x_i – m)²/2s²]},

where m determined by the prior distribution, the x_i are five observed numbers, and s² = 1. Then, after some algebra (see Problem 3.3.6), the posterior can be written as

f(m|x) µ f(m)f(x|m) µ exp [–(m – m_n)²/2V_n],

which is the kernel of N(m_n, V_n), where

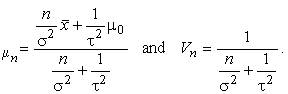
It is common to use the term precision to refer to the reciprocal of a variance. Using this terminology, we say that m_n is a weighted average of the prior mean and the sample mean, where the precisions are the weights.

Here the precision of each observation is much greater than the precision of the prior. In this case even our small sample of five observations is enough to diminish the impact of the prior on the posterior distribution.

3.3.3. Example 3 (counting mice) continued

Suppose that a region of the island is selected where the gamma prior distribution with parameters a = 4 and b = 3 is reasonable. This prior has density f(l) µ l^a^{- 1}e^–l/^b. Over a period of about a year traps are set out on n = 50 nights with total number of captures T = S x_i = 256, for an average of 5.12 mice captured per night. This gives the likelihood

Thus, the posterior distribution f(l|x) is gamma with parameters given by a_n = T + a = 260 and 1/b_n = n + 1/b = 50 + 1/3, so that b_n = 0.0199. A 95% Bayesian probability interval for l based on this posterior distribution is (4.56, 5.82).

Problems

3.3.1. This problem deals with point and interval estimates of the population proportion in the continuation of Example 1.

(a) It might be reasonable to use the mode of the posterior distribution as a point estimate of the proportion in favor of Proposition A in the population. What is its numerical value?

(b) Use a computer package to verify the endpoints of the Bayesian probability interval given in the Section 3.3.2. This is a probability-symmetric interval which excludes 2.5% of the probability in each tail of the posterior distribution.

(c) Taking a frequentist point of view, use the normal approximation to the binomial distribution to find an approximate 95% confidence interval for the population proportion. What is the main difference between this interval and the one verified in part (a)?

(d) What Bayesian point estimate (mode) and 95% probability interval would have resulted from using the uniform distribution on (0, 1) as the prior distribution?

3.3.2. This problem deals with point and interval estimates of m in Example 2. Suppose that the five measurements of the weight of the beam are: 198.14, 198.45, 196.59, 197.64, 198.12 (mean 197.79).

(a) What is the point estimate of m. In this instance, does it matter whether we choose the mean, the median, or the mode of the posterior distribution as our point estimate? Explain.

(b) Find a 95% Bayesian probability estimate of m.

(c) Suppose we would be unwilling to use this beam for a particular purpose if we thought it weighed less than 197 lb. What are the chances of that?

(d) Taking a frequentist point of view, use the five observations and the known variance of measurements produced by the scale to give a 95% confidence interval for the true weight of the beam.

(e) What Bayesian point estimate and 95% probability interval would have resulted from using a normal distribution with mean 202 and standard deviation 5 as the prior?

3.3.3. This problem deals with point and interval estimates of l in Example 3 based on the data given in Sec. 3.3.3.

(a) Find the mean, median, and mode of the posterior distribution.

(b) Verify the 95% Bayesian probability interval given in Sec. 3.3.3. Strictly speaking, shorter 95% probability intervals can be found because of the skewness of the distribution. For such a shorter interval would slightly more or slightly less that 2.5% be omitted from the right tail?

(c) Taking a frequentist point of view, find an approximate 95% confidence interval for nl and hence for l. Use the fact that T has a Poisson distribution that is well-approximated by an appropriate normal distribution.

(d) Suppose that the prior distribution had been gamma with parameters a = 3 and b = 1. Give an interval that contains 95% of the probability under this prior distribution. Use the same data as above (T = 256) and find the corresponding 95% Bayesian probability interval for l.

3.3.4. Derive the posterior distribution resulting from a beta prior and binomial data. Verify the specific parameter values given in Sec. 3.3.1.

3.3.5. Derive the posterior distribution resulting from a gamma prior and Poisson data. Verify the specific parameter values given in Section 3.3.3. (The gamma prior is conjugate to the Poisson distribution of the data.)

3.3.6. In this problem we invite you to derive the posterior distribution for Example 2 in Section 3.3.2.

(a) Show that the expression f(x|m) µ exp {–S[(x_i – m)²/2s²]} for the likelihood function is correct and can be re-expressed as

The likelihood function is the joint density function of the data viewed as a function of m (rather than of the x_i). By independence, the joint density function is proportional to P exp{–[(x_i – m)²/2s²]}, which is clearly equal to the first expression for the likelihood function. To put the first expression in the form displayed just above, write

expand the square and sum over i. On distributing the sum you should obtain three terms. One of the terms provides the desired result; another is 0, and the third is irrelevant because it does not contain the variable m. (A constant term in the exponential amounts to a constant factor in the density, which is not included in the kernel.)

(b) Derive the expression for the kernel of the posterior given in Section 3.3.2. Multiply the kernels of the prior and the likelihood, and expand the squares in each. Put everything in the exponential over a common denominator. Then, remembering that m is the variable, collect terms in m² and m. Terms in the exponent that do not involve m are constant factors in the posterior density that may be adjusted at will to complete the square in order to obtain the desired kernel.

3.4. More About Prior Distributions

One issue of concern in Bayesian inference is how strongly the particular selection of a prior distribution influences the results of the inference. Particularly if results are to be used by people who may question the expert's opinion, it is desirable to have enough data that the influence of the prior is slight.

An uninformative prior (sometimes called a flat prior) is one that provides little or no information. Depending on the situation, uninformative priors may be quite disperse, may avoid only impossible or quite preposterous values of the parameter, or may not have modes. Uninformative priors sometimes give results similar to those obtained by traditional frequentist methods.

Returning once again to our election example, the first row of the table below summarizes a prior that matched the expert's opinion, the posterior, and our inference. Now suppose that another expert also believes that Proposition A is more likely than not to pass, but his views about current public opinion are more vague. Perhaps his beta prior has parameters 56 and 46. This prior also has mode 55%, but here the prior has P(0.45 < P < 0.64) = 0.95. Without seeing any data, the second expert gives Proposition A a non-trivial chance of losing if the election were held today: P(P < 0.5) = 0.16.

After he sees the results of the poll with 621 out of 1000 in favor, his posterior beta distribution has parameters 677 and 425, so that his 95% posterior interval estimate is (59.5%, 65.2%), as recorded in the second row of the table.

The reasonable choice for an uninformative prior in this situation is the uniform distribution (which is beta with parameters 1 and 1, and which has no mode); it gives the 95% posterior interval estimate (59.1%, 65.1%).

In this example, the 1000 observations are enough data that the two expert priors and the uninformative prior all give somewhat similar results. (The agreement would not be so good with a small amount of data.) A non-Bayesian 95% confidence interval, based on the normal approximation, is (59.1%. 65.1%).

Beta Prior Parameters	Mode of Prior Distribution	Prior 95% Prob. Interval	Mode of Posterior Distribution	Posterior 95% Prob. Interval
a = 331, b = 271	55	(51.0%, 59.0%)	56.4%	(57.0%, 61.8%)
a = 45, b = 46	55	(45.0%, 64.0%)	61.5%	(59.5%, 65.2%)
a = 1, b = 1	No Mode	(2.5%, 97.5%)	62.1%	(59.1%, 65.1%)
Frequentist	(No Prior)	(No Prior)	^p = 62.1%	CI: (59.1%, 65.1%)

Notice that, in view of the polling results, both experts were a little too pessimistic about the prospects for Proposition A. However, the first expert's "sharper" prior (first row of the table) is roughly equivalent in influence to surveying 600 people and so the results of the actual survey of 1000 people are not enough to override this expert's view that the true percentage in favor is unlikely to be above 60%. The second expert's somewhat "flatter" prior (second row) is roughly equivalent in influence to surveying 100 people and the actual survey results from 1000 people nearly override his opinion.

The uninformative prior (uniform distribution in the third row) gives a mode and probability interval that agree with the frequentist point estimate and confidence interval. However, the philosophical bases of Bayesian and frequentist methods differ, as do the interpretations of the results. The Bayesian results are statements about a posterior distribution for the particular situation at hand, whereas the frequentist results must be interpreted in terms of many hypothetical repetitions of the sampling experiment. If the frequentist results depend on prior experience, it is by way of the design of the survey, whereas the Bayesian results can depend explicitly on personal probability assessments.

Problems

3.4.1. The table of this section shows four rows with various point and interval estimates for the election example. Make a similar table for the beam weight example. Use the data of Problem 3.3.2: 198.14, 198.45, 196.59, 197.64, 198.12 (mean 197.79). In the first row show results for the prior N(200, 10²), and in the second row results for the prior N(202, 5²). There is no such thing as a truly uninformative normal prior, but select a normal prior for the third row that gives results numerically similar (to two decimal places) to frequentist results, which you should show in the fourth row. Summarize and comment upon the results shown in the table, making any extra rows that you think would add to your understanding of this example.

3.4.2. The table of this section shows four rows with various point and interval estimates for the election example. Make a similar table for the mouse counting example. Suppose, as in Section 3.3.3 that 256 mice altogether are trapped in 50 nights. In the first row show results for the gamma prior distribution with parameters a = 4 and b = 2, and in the second row results for the gamma prior with a = 2 and b = 5. There is no such thing as a truly uninformative gamma prior, but see if you can find a gamma prior for the third row that gives results numerically similar (to two decimal places) to frequentist results, which you should show in the fourth row. Summarize and comment upon the results shown in the table, making any extra rows that you think would add to your understanding of this example.

Copyright © 2000 Bruce E. Trumbo. All rights reserved. Intended mainly for instructional use at California State University, Hayward. This is a draft; comments and corrections are welcome. To request permission for other uses please contact btrumbo@csuhayward.edu.

Session 4: A Brief Introduction To Bayesian Estimation

3.1. Introduction

3.2. Prior Distributions: Personal Opinions and Expert Knowledge

Problems

3.3. Data and Posterior Distributions

3.4. More About Prior Distributions

Session 4: A Brief Introduction
To Bayesian Estimation